สำหรับการเคลื่อนที่แบบวงกลมนั้น ถือว่าเป็นกรณีเฉพาะกรณีหนึ่งของการเคลื่อนที่แบบหมุน ทีนี้เราจะสนใจกรณีทั่วๆไปของการเคลื่อนที่แบบหมุนว่ามีลักษณะเป็นอย่างไร และมักจะนำมาเปรียบเทียบกับการเคลื่อนที่แบบเส้นตรง ทั้งกรณีความเร็วคงที่ และกรณีความเร็วไม่คงที่ (มีความเร่งแบบคงที่)

กรณีที่ 1 การเคลื่อนที่แบบหมุนด้วยอัตราคงที่

จะมีปริมาณที่เกี่ยวข้องคล้ายๆกับการเคลื่อนที่แบบเส้นตรง ดังนี้

1.มุม (angle) มักใช้สัญลักษณ์เป็น \theta เป็นค่าแสดงถึงว่า “วัตถุมีการเปลี่ยนตำแหน่งจากเดิมไปด้วยมุมเท่าใดจากเดิม”

ปริมาณที่เกี่ยวข้องกับการเคลื่อนที่แบบหมุน
มุม อัตราเร็วเชิงมุม ความเร็วเชิงมุม และความเร่งเชิงมุม

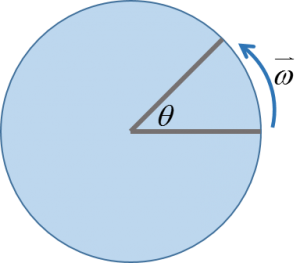
สมการการเคลื่อนที่แบบหมุน

2.อัตราเร็วเชิงมุม (angular speed) : \omega

  • หมายถึง มุมที่วัตถุเปลี่ยนตำแหน่งจากเดิม เมื่อเทียบกับหนึ่งหน่วยเวลา เป็นปริมาณสเกลาร์ หรือเขียนเป็นสมการได้ ดังนี้

\omega = \frac{\Delta\theta}{\Delta t}

3.ความเร็วเชิงมุม (angular velocity) : \overrightarrow{\omega}

  • หมายถึง มุมที่วัตถุเปลี่ยนตำแหน่งจากเดิม เมื่อเทียบกับหนึ่งหน่วยเวลา เป็นปริมาณเวกเตอร์ โดยทิศทางที่เราสนใจอาจจะเป็นในรูปแบบ ตาม หรือ ทวน เข็มนาฬิกา ดังนี้

\overrightarrow{\omega} = \frac{\Delta\overrightarrow{\theta}}{\Delta \overrightarrow{t}}

4. ความเร่งเชิงมุม (angular acceleration) : \overrightarrow{\alpha}

  • หมายถึง ความเร็วเชิงมุมที่เปลี่ยนแปลงไป เมื่อเทียบกับหนึ่งเวลา เป็นปริมาณเวกเตอร์ เขียนเป็นสมการได้ ดังนี้

\overrightarrow{\alpha} = \frac{\Delta\overrightarrow{\omega}}{\Delta \overrightarrow{t}}

Related posts:

  1. การเคลื่อนที่แนวตรง       ในการศึกษาฟิสิกส์ระดับมัธยมศึกษา เราจะแบ่งลักษณะการเคลื่อนที่ที่ต้องการศึกษาไว้หลักๆ 2 แนว คือ ...
  2. การเคลื่อนที่แบบหมุน 2      สำหรับการเคลื่อนที่แบบมีความเร่งคงที่ของการเคลื่อนที่แนวเส้นตรง จะใช้สมการ ดังตารางในคอลัมภ์แรก ...
  3. คณิตศาสตร์สำหรับฟิสิกส์ 3 1. เวกเตอร์ในระบบพิกัดฉาก       เราทราบแล้วว่าเวกเตอร์เป็นปริมาณที่มีทั้งขนาดและทิศทาง ในทางคณิตศาสต ...
  4. ปริมาณทางฟิสิกส์ ปริมาณทางฟิสิกส์ แบ่งออกเป็น 2 ประเภท ได้แก่ ปริมาณสเกลาร์ และปริมาณเวกเตอร์...
  5. ของไหลและความดันในของไหล ของไหล หรือ Fluid มีความหมายรวมถึงสสารที่อยู่ในสถานะของเหลว แก๊ส แต่ในบางครั้งของไหลบางชนิดมีความหนื ...
  6. แรงลอยตัว หรือแรงพยุง (Buoyant Force) เมื่อวัตถุจมอยู่ในของไหล ไม่ว่าจะเป็นแก๊ส หรือของเหลวก็ตามจะมีแรงพยุงกระทำกับวัตถุนั้นเสมอ...
  7. เนื้อหากลศาสตร์แบบดั้งเดิม หัวข้อ ฟิสิกส์มัธยมศึกษา 1. บทนำ  ประวัติศาสตร์การวัด  หน่วย SI  หน่วยฐาน (Based ...
  8. เนื้อหาวิชาฟิสิกส์ (Physics Story) เนื้อหาฟิสิกส์มอปลาย ระดับชั้นมัธยมศึกษาปีที่ 4, 5 และ 6 เหมาะสำหรับการอ่านทบทวน หมวดหมู่เนื้อหา (Co ...