กฎของปาสคาล และเครื่องอัดไฮดรอลิก

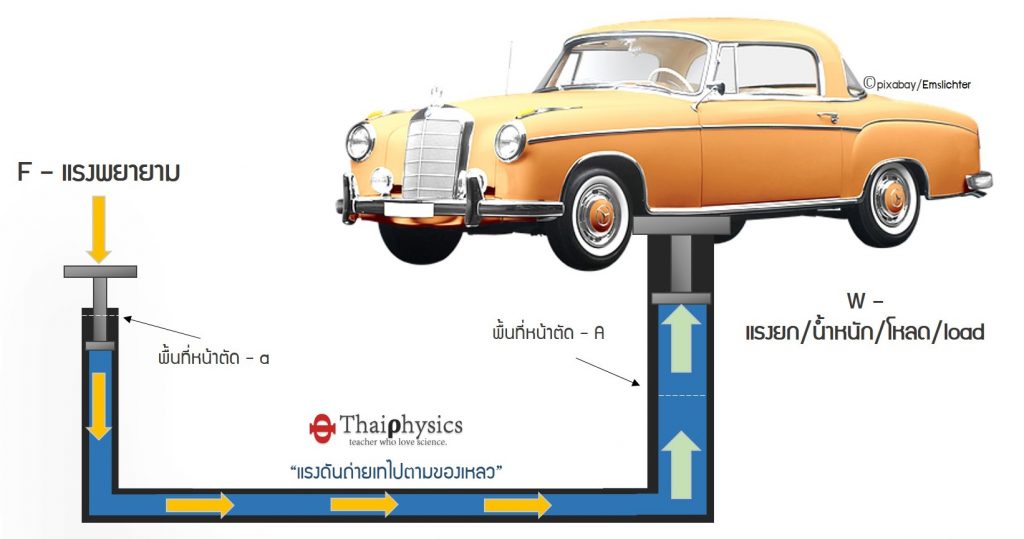
หนึ่งในกฎที่สำคัญสำหรับการศึกษาของไหล (Fluid) โดยเฉพาะของไหลที่เปลี่ยนปริมาตรได้ยากอย่าง “ของเหลว (Liquid)” นั่นก็คือกฎของปาสคาล (Pascal’s Law)

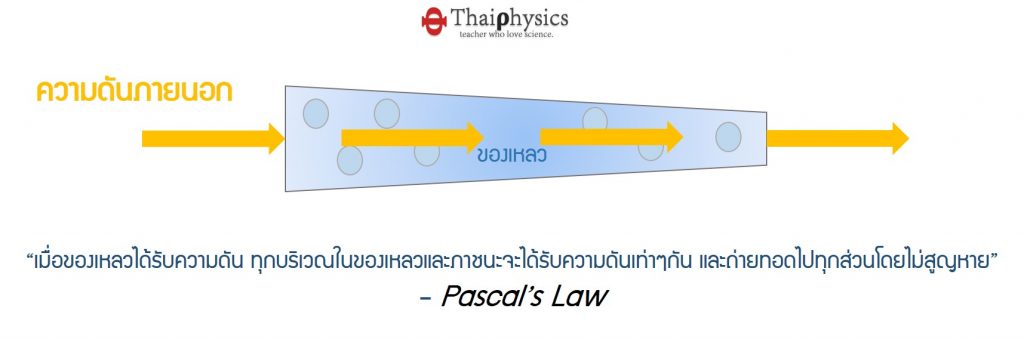
ใจความสำคัญของกฎของปาสคาลคือ

ใช้งานได้ดี หรืออธิบายปรากฏการณ์เกี่ยวกับของไหลได้เฉพาะ “ของเหลว” แต่เพียงเท่านั้น เนื่องจากปริมาตรของของเหลวเปลี่ยนไปน้อยมาก เมื่อได้รับความดัน (แก๊สมักเปลี่ยนปริมาตรเมื่อได้รับความดัน)
หากในภาชนะที่บรรจุของเหวไม่มีแก๊สผสม หรือฟองอากาศ ความดันจะถ่ายทอดไปทุกๆ บริเวณในของเหลว รวมทั้งผนังภาชนะอีกด้วย
ความดันที่ถูกถ่ายทอดไปนั้นไม่สูญหาย

เนื้อหา :

การประยุกต์ใช้กฎของปาสคาล

หนึ่งในสิ่งประดิษฐ์ที่นิยมพูดถึงเกี่ยวกับกฎของปาสคาล นั่นก็คือ เครื่องอัดไฮดรอลิก (Hydraulic Press Machine) โดยเป็นเครื่องมือถ่ายทอดแรงดันผ่านของเหลวที่บีบอัดได้ยาก หรือไม่ได้เลย ทำให้เกิดแรงดันที่ปลายอีกด้านหนึง

ของเหลวที่มักบรรจุในสายไฮดรอลิก ก็คือ น้ำมันไฮดรอลิก

จากรูป เมื่อออกแรงพยายาม F ในการยกรถที่มีน้ำหนัก W ความดันที่ถ่ายเทไปตามของเหลวจะไม่มีการสูญหาย แสดงว่าความดันปลายทั้งสองของสายไฮดรอลิกต้องมีขนาดเท่ากัน

$P_{left} = P_{right}$

$\frac{F}{a} = \frac{W}{A}$

$\frac{W}{F}= \frac{A}{a}$

เราเรียกอัตราส่วน $\frac{W}{F}$ ว่า “การได้เปรียบเชิงกลเชิงปฏิบัติ”

และเรียกอัตราส่วน $\frac{A}{a}$ ว่า “การได้เปรียบเชิงกลเชิงทฤษฎี” (พื้นที่ไม่มีทางเปลี่ยนขนาดได้)

ประสิทธิภาพเชิงกล (Mechanical Advantage : MA)

เมื่อต้องการที่จะตรวจสอบว่าระบบหรือเครื่องกลมีประสิทธิภาพเพียงใด ต้องพิจารณางานที่ระบบทำได้ เทียบกับงานที่ใส่ให้กับระบบ ดังสมการ

$eff_{MA} = \frac{Work_{out}}{Work_{in}}$

หรือคิดเป็นเปอร์เซนต์ได้ดังนี้

$\% eff_{MA} = \frac{Work_{out}}{Work_{in}} \times 100\%$

หากการใส่งานให้กับระบบเกิดพร้อม ๆ กับที่ระบบให้งานกลับมาสามารถหาประสิทธิภาพเชิงกลได้จากเทอมของกำลัง (Power) ได้เช่นกัน

$\% eff_{MA} = \frac{P_{out}}{P_{in}} \times 100\%$

การประยุกต์ใช้กฎของปาสคาล

ประสิทธิภาพเชิงกล (Mechanical Advantage : MA)

Related posts:

ตรวจพบ Ad Blocker