การเคลื่อนที่แบบวงกลมในแนวดิ่ง

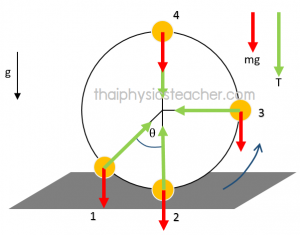
สมการการเคลื่อนที่แบบวงกลมในแนวดิ่ง

ตำแหน่งที่ 1 : แรงตึงเชือก T และ แรงเนื่องจากน้ำหนักของวัตถุ $mgcos\theta$ หักล้างกัน โดยที่แรง T มีขนาดมากกว่า ทำให้เกิดแรงเข้าสู่ศูนย์กลาง ดังสมการ (ต้องแตกแรงให้อยู่ในแนวเดียวกัน ในทีนี้คือแนวเส้นรัศมี)

$\Sigma F = ma$

$T - mgcos\theta = m\frac{v^2}{R}$

$T_1 = m\frac{v^2}{R} + mgcos\theta$

ตำแหน่งที่ 2 : แรงตึงเชือก T และ แรงเนื่องจากน้ำหนักของวัตถุ mg หักล้างกัน โดยที่แรง T มีขนาดมากกว่า ทำให้เกิดแรงเข้าสู่ศูนย์กลาง ดังสมการ

$\Sigma F = ma$

$T - mg = m\frac{v^2}{R}$

$T_2 = m\frac{v^2}{R} + mg$

ตำแหน่งที่ 3 : สำหรับตำแหน่งนี้จะมีแค่แรงตึงเชือก T เพียงแรงเดียวที่ทำหน้าที่เป็นแรงเข้าสู่ศูนย์กลาง ดังสมการ

$\Sigma F = ma$

$T_3 = m\frac{v^2}{R}$

ตำแหน่งที่ 4 : แรงตึงเชือก T และ แรงเนื่องจากน้ำหนักของวัตถุ mg เสริมกัน เนื่องจากมีทิศทางเดียวกัน (ชี้ลง) จะได้ว่า

$\Sigma F = ma$

$T + mg = m\frac{v^2}{R}$

$T_4 = m\frac{v^2}{R} - mg$

เพื่อพิจารณาแรงตึงเชือกในแต่ละตำแหน่งจะได้ว่า $T_2 > T_1 >T_3 >T_4$ ทั้งนี้อยู่ภายใต้สมมติฐานที่ว่าความเร็วของวัตถุมีค่าใกล้เคียงกัน (ค่า v ไม่แตกต่างกันมาก หากหมุนด้วยความเร็วสูง)

ข้อสังเกต ทำไมแรงตึงเชือก T ต้องมากกว่า mg?

ลองมองในแง่ความจริง หากแรง mg มีค่ามากกว่า เชือกต้องขาด! แต่ ณ ตอนนี้เราพิจารณาการเคลื่อนที่แบบวงกลม โดยมีวัตถุผูกติดอยู่กับเชือกเคลื่อนที่ในแนวดิ่ง เช่นนั้นแล้วแรงตึงเชือก T ต้องมากกว่า mg (โดยเฉพาะตำแหน่งที่ 1 และ 2)

Related posts:

ตรวจพบ Ad Blocker