มุมที่ทำให้วัตถุตกในระยะไกลสุด

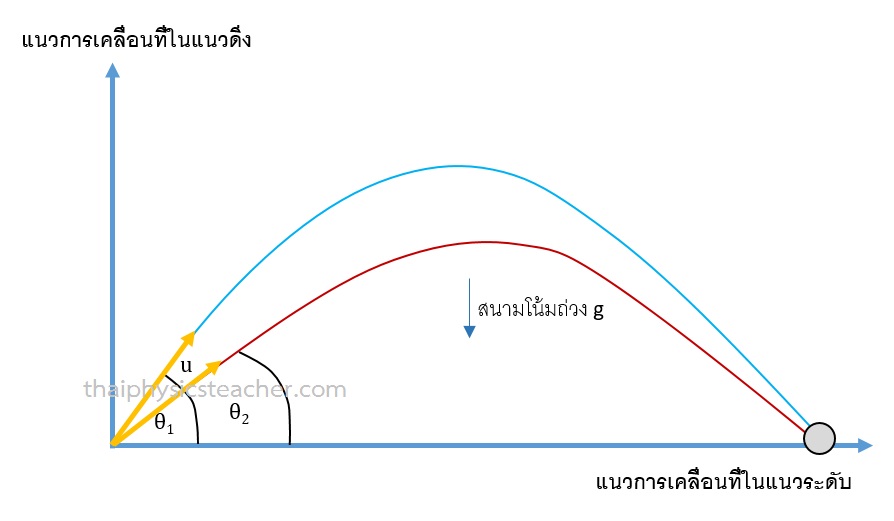
การหามุมที่ทำให้วัตถุตกไกลสุดของ การเคลื่อนที่แบบโพรเจกไทล์

เนื้อหา :

1. มุมสองมุมที่เมื่อยิงออกไปจะทำให้วัตถุตกในระยะเท่ากัน

ในการเคลื่อนที่แบบโพรเจกไทล์จะมีมุมอยู่ 2 ค่าที่ทำให้วัตถุตกเป็นระยะเท่ากัน แต่ต้องยิงด้วยอัตราเร็วต้นขนาดเท่ากัน หรือ u คงที่ และพบว่ามุมสองมุมนั้นจะรวมกันได้ค่า 90 องศาทุกครั้ง

$\theta_1 + \theta_2 = 90^{\circ}$

2. การพิสูจน์มุมที่ทำให้วัตถุตกไกลสุด การเคลื่อนที่แบบโพรเจกไทล์

ในการเคลื่อนที่แบบโพรเจกไทล์เราพบว่ามุมที่ทำให้วัตถุตกในระยะไกลที่สุด มีค่าเท่ากับ 45 องศา ด้วยเหตุดังนี้

จากสมการ $s_x = u_xt \colon s_y = u_yt + \frac{1}{2} gt^2$

เนื่องจากวัตถุตกถึงพื้นแล้วทำให้การกระจัดในแนวดิ่ง $s_y = 0$ จะได้ $0 = u_yt + \frac{1}{2}gt^2 \rightarrow t = \frac{2u_y}{g} \rightarrow t = \frac{2u\sin\theta}{g}$

แต่ $s_x = u_xt = u\cos\theta t$ นำ $t = \frac{2u\sin\theta}{g}$ แทนใน $s_x = u_xt = u\cos\theta t$

จะได้ $s_x = u\cos\theta ( \frac{2u\sin\theta}{g} = \frac{u^22\sin\theta\cos\theta}{g}$

แต่ $2\sin\theta\cos\theta = \sin{2}\theta$ จะได้ $s_x = \frac{u^2\sin{2}\theta}{g}$

เนื่องจาก u และ g คงที่ ฉะนั้นหากต้องการให้ $s_x$ มีค่ามากที่สุดพบว่า $\sin{2}\theta = 1$

หรือ $2\theta = 90^\circ$ หรือ $\theta = 45^\circ$

1. มุมสองมุมที่เมื่อยิงออกไปจะทำให้วัตถุตกในระยะเท่ากัน

2. การพิสูจน์มุมที่ทำให้วัตถุตกไกลสุด การเคลื่อนที่แบบโพรเจกไทล์

Related posts:

ตรวจพบ Ad Blocker