เส้นสนามไฟฟ้า และจุดสะเทินในสนามไฟฟ้า

เนื้อหา :

เส้นสนามไฟฟ้า

เส้นสนามไฟฟ้า เป็นเส้นสมมติที่ถูกเขียนขึ้น เพื่อแสดงทิศทางของสนามไฟฟ้าในบริเวณรอบๆ ประจุไฟฟ้า

การพิจารณาขนาดสนามไฟฟ้า แบ่งออกเป็น 2 ลักษณะ

1. บริเวณที่มีเส้นสนามไฟฟ้าหนาแน่นมาก สนามไฟฟ้าที่บริเวณนั้นมีค่ามาก

2. บริเวณที่มีเส้นสนามไฟฟ้าหนาแน่นน้อยสนามไฟฟ้ามีค่าน้อย

เส้นสนามไฟฟ้าที่มีความหนาแน่นสม่ำเสมอ สนามไฟฟ้าในบริเวณดังกล่าวจะมีค่าสม่ำเสมอ สนามไฟฟ้าเนื่องจากแผ่นตัวนำที่ขนานกันที่มีประจุต่างชนิดกันเป็นสนามไฟฟ้าสม่ำเสมอ

จุดสะเทินในสนามไฟฟ้า

เส้นสนามไฟฟ้าและจุดสะเทิน ฟิสิกส์ — สัญลักษณ์กากบาทบริเวณระหว่างจุดประจุบวกคือบริเวณที่ไม่มีสนามไฟฟ้า เนื่องจากมีการหักล้างกันหมด

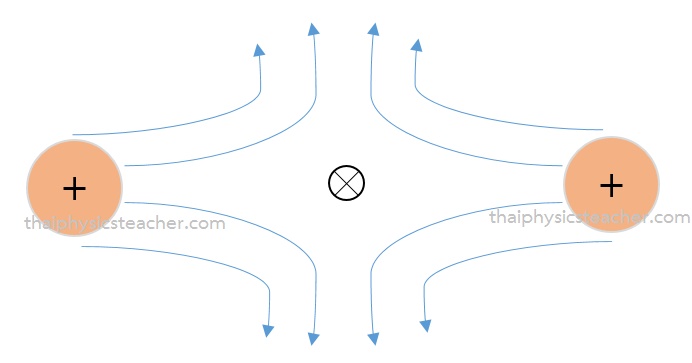
จุดสะเทิน หมายถึง จุดใดๆ ในสนามไฟฟ้า ซึ่งมีค่าของสนามไฟฟ้าลัพธ์เป็นศูนย์ เนื่องจากจุดนั้นอาจปรากฏมีสนามไฟฟ้าอย่างน้อยที่สุดของสนาม 2 สนามที่ที่มีค่าของสนามไฟฟ้าเท่ากันแต่ทิศทางตรงกันข้ามหรือ ณ จุดนั้นมีสนามไฟฟ้ามากกว่า 2 สนามแต่ค่าของสนามไฟฟ้าและทิศทางของสนามไฟฟ้าเหล่านั้นอยู่ในลักษณะที่สนามไฟฟ้าหักล้างกันหมด

กล่าวโดยสรุป คือ จุดสะเทิน เป็นบริเวณที่ไม่มีสนามไฟฟ้า เนื่องจากทิศทางของสนามไฟฟ้า 2 บริเวณขึ้นไปมีทิศทางตรงกันข้ามกัน และขนาดพอๆกัน หรือขนาดพอดีที่ทำให้สนามไฟฟ้าหักล้างกันหมด

การคำนวณหาจุดสะเทิน

กรณีที่ 1 จุดประจุขั้วเดียวกัน ขนาดเท่ากัน

ถ้ากำหนดให้จุดประจุสองอันมีขั้วเดียวกัน และขนาดเท่ากัน สมมติเป็นประจุ +q ดังรูป

จุดสะเทินของจุดประจุขั้วเดียวกันขนาดเท่ากัน — การคำนวณหาจุดสะเทินของประจุขั้วเดียวกันและขนาดเท่ากัน Author: thaiphysicsteacher

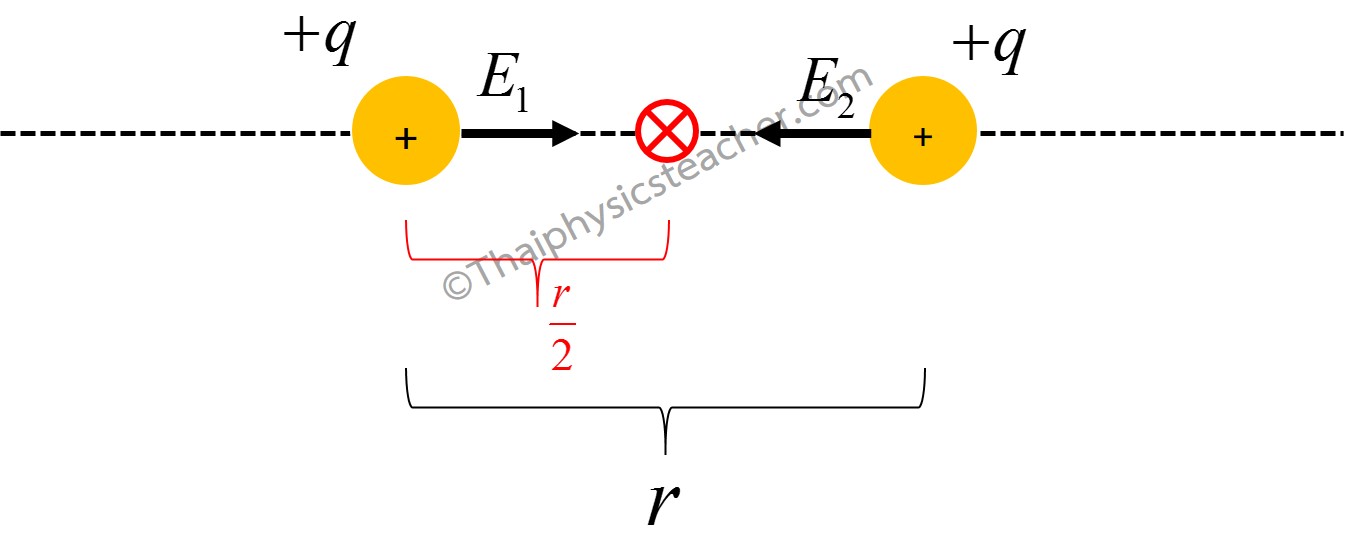
เราสามารถคำนวณหาจุดสะเทิน หรือจุดที่ไม่มีสนามไฟฟ้า (E = 0) ได้ดังนี้

ให้ $E_1$ แทนสนามไฟฟ้าอันเนื่องมาจากประจุ +q ตัวหนึ่ง

และ $E_2$ แทนสนามไฟฟ้าอันเนื่องมาจากประจุ +q อีกตัว

จากคำนิยามของจุดสะเทิน ซึ่งหมายถึง จุดหรือบริเวณเล็กๆที่ผลรวมของสนามไฟฟ้าย่อยเนื่องจากประจุแต่ละตัวเท่ากับศูนย์

หรือ $\Sigma{E} = 0$

จะได้ว่า $E_1 - E_2 = 0$

$E_1 = E_2 --(1)$

และจาก $E = \frac{kq}{r^2}--(2)$

นำสมการที่ (2) แทนในสมการที่ (1) จะได้ว่า

$\frac{kq_1}{{r_1}^2} = \frac{kq_2}{{r_2}^2}$ โดยที่ r คือระยะห่างใดๆจากจุดสะเทินจากจุดประจุแต่ละตัว

แต่เนื่องจาก $q_1 = q_2$ จะได้ว่า $\frac{1}{{r_1}^2} = \frac{1}{{r_2}^2}$

หรือ จะได้ว่า $r_1 = r_2$ โดยสมการนี้หมายถึงจุดสะเทินจะอยู่ห่างจากประจุแต่ละตัวเท่ากัน

และหากพิจารณาจากรูปก่อนหน้า คงไม่มีจุดไหนที่จะอยู่ห่างจากจุดประจุแต่ละตัว แล้วทำให้เกิดจุดสะเทินได้อีก

นอกจากจุดที่ห่างจากประจุแต่ละตัวเป็นระยะ $\frac{r}{2}$

Previous Page : สนามไฟฟ้า

Next Page : สนามไฟฟ้าของโลหะคู่ขนาน

ตรวจพบ Ad Blocker

เว็บไซต์ของเราเชื่อมั่นในประสบการณ์ในการรับชมของผู้ชม แต่อย่างไรก็ตามเว็บไซต์จะขับเคลื่อนไปได้ เมื่อได้รับการสนับสนุนจากผู้ลงโฆษณา โปรดพิจารณายกเลิกส่วนเสริม (Extension) Ad Blocker สำหรับ Domain Site นี้ ขอบคุณครับOur website is made possible by displaying online advertisements to our visitors. Please consider supporting us by disabling your ad blocker.